CS/Data Structure
[ DS ] Heap
KimBangg
2021. 8. 10. 19:54
1. Heap
- 우선순위가 높은 요소가 먼저 나가는 특징을 가진다.
- 루트가 가장 큰 값이 되는 최대 힙과 루트가 가장 작은 값이 되는 최소 힙이 있다.
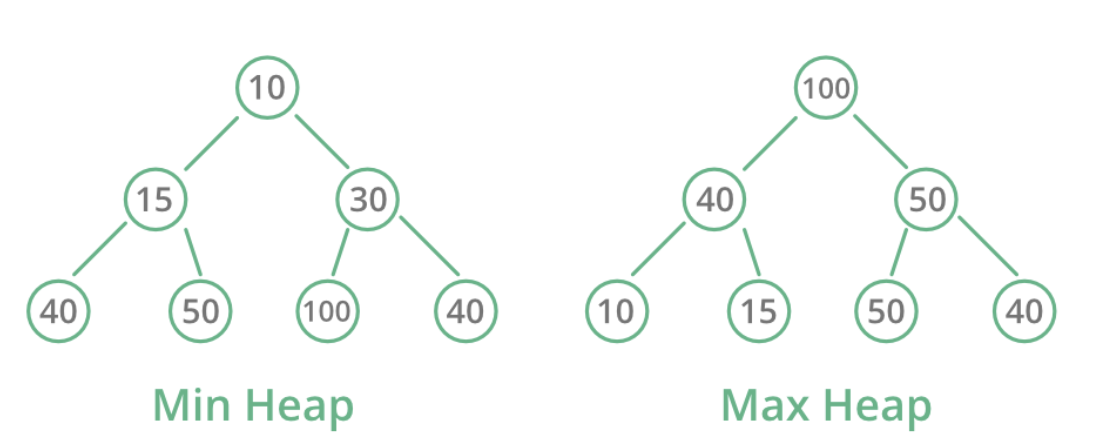
2. 힙 추가
- 요소가 추가 될 때는 트리의 가장 마지막 정점에 위치한다.
- 추가 후 부모 정점보다 우선순위가 높다면 부모 정점과 순서를 바꾼다.
- 완전 이진 트리의 높이는 log n 이기에 힙의 요소 추가 알고리즘은 O(log n) 시간복잡도를 가진다.
class maxHeap {
constructor() {
this.heap = [null];
}
push(value) {
// 힙에 가장 끝에 추가
this.heap.push(value);
let currentIdx = this.heap.length - 1;
let parentIdx = Math.floor(currentIdx/2);
// 부모가 우선 순위가 아니고, 루트가 아니면
while ( parentIDx !== 0 && this.heap[parentIdx] < value ) {
const temp = this.heap[parentIdx];
this.heap[parentIdx] = value;
this.heap[currentIdx] = temp;
currentIdx = parentIdx;
parentIdx = Math.floor(currentIdx/2);
}
}
}
3. 힙 제거
- 요서 제거는 루트 정점만 가능합니다..
- 루트가 제거된 후 가장 마지막 정점이 루트로 이동합니다.
- 루트 정점의 두 자식 정점 중 더 우선 순위가 높은 정점과 자리를 바꿉니다.
- 두 자식 정점이 우선 순위가 더 낮을 떄 까지 반복합니다.
- 시간복잡도는 O(log n)만큼 소요됩니다.
pop() {
// 루트 요소를 반환 하기 위해 상수로 저장.
const returnValue = this.heap[1];
// 루트 정점을 마지막 정점으로 대체한다.
this.heap[1] = this.heap.pop();
// 아래로 내려가면서 검사 할 떄 사용하는 인덱스
let currentIdx = 1;
let leftIdx = 2;
let rightIdx = 3;
// 하위 요소의 우선순위보다 현재 우선순위가 높으면 종료
while (
this.heap[currentIdx] < this.heap[leftIdx] || this.heap[currentIdx] < this.heap[rightIdx]
) {
// 오른쪽 정점이 우선 순위가 더 높은 경우
if ( this.heap[leftIdx] < this.heap[rightIdx]) {
const temp = this.heap[currentIdx];
this.heap[currentIdx] = this.heap[rightIdx];
this.heap[rightIdx] = temp;
currentIdx = rightIdx;
}
else { // 왼쪽 정점이 더 높은 경우
const temp = this.heap[currentIdx];
this.heap[currentIdx] = this.heap[leftIdx];
currentIdx = leftIdx
}
// 좌, 우 인덱스 재 설정.
leftIdx = currentIdx * 2;
rightIdx = currentIdx * 2 + 1;
}
return returnValue;
}